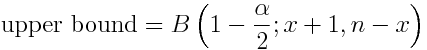Reporting binomial proportion confidence intervals
As search marketing experts we often need to make comparisons between different populations. For example; testing the conversion rate of one advert or landing page against another, and there are established, robust and well understood ways of doing so (chief of which is probably a chi-squared test for independence). We use this type of analysis to take decisions on changing ad texts, comparing strategies, and when making other comparisons.
We perhaps do less well when reporting a single binomial proportion. Click through rates, conversion rates and bounce rates are all examples of binomial proportions. The term binomial just refers to there being two distinct possibilities – click or don’t click, bounce or interact, etc.
The problem
How confident can we be in the click-through rate we witness for a PPC campaign after only 100 impressions? What about 100,000 impressions? Do we suspect from experience that the recent click-through rate was particularly high and we only have a small sample size? How can we communicate this to a client?
Consider a concrete example: What should we report if the client asks us what the conversion rate is on their new landing page? It has attracted 250 visitors and made 5 conversions.
We must be cautious here not to simply stipulate that the new landing page has a conversion rate of 2%. 2% is only our best estimate at what the page’s conversion rate may be. It should be made clear that we do not have enough data to assert that this sample conversion rate will apply to the larger population. We should be very careful what we report to our client in these circumstances. The term ‘conversion rate’ without further explanation could imply a known rate that we expect to continue into the future. We cannot assert that without a much larger sample of data. It is part of our day job to know that, in this example, we do not really have a large enough sample to base modelling decisions on – our client may not always have that statistical knowledge or experience.
So how much data do we need? We could reasonably expect any moderately proficient high school maths student to be able to calculate the sample conversion rate witnessed for the landing page but surely we should be doing better? Following the same precept, if our client asks us for details of their conversion rates for some top keywords do we lazily export a report from AdWords and let them make of it what they will?
We should remember that the client is paying for our expertise. It is neither learned nor skilled to export a report and email it off. Nor is it particularly skilled to calculate a simple sample proportion. Perhaps we should consider more carefully the purpose of the data we are reporting? Perhaps the client just wants some headlines about the performance of the campaign and showing the report as is would be OK, but what if the client wants to spend a significant sum of money promoting a website? We do not want them unknowingly running a risk of basing decisions on a random spike (or dip) in the data. Or what if they are thinking about pulling a campaign based on data with a sample size too small to be significant? It is incumbent upon us to explore the client’s intentions and to guard against these scenarios by providing meaningful advice and statistical analysis on the raw data we present.
Significance values or confidence intervals
So what statistical analysis should we report to guide the client on how confident we can be in the given sample? There are two main possibilities:
- Significance Scores
- Confidence Intervals
The former provides a score or p-value representing the probability of obtaining a further sample that is at least as far from the true underlying proportion as the sample we are testing.
The latter, which is arguably much easier to describe as well as to interpret, takes as a parameter a confidence level (say 95%) and provides a range of values which we can be confident the true underlying proportion will lay within.
Many statisticians, including Gardner and Altman in [1], argue (convincingly!) that the latter is more readily interpreted and it would be hard to make any real case to the contrary. Which of these statements would you rather include in a presentation or a report for a client?
- “We have witnessed a 12% conversion rate so far and, based on statistical analysis, we can be 95% certain that the true conversion rate lies between 11.2% and 13.1%”
- “We have witnessed a 12% conversion rate so far and the sample dataset has a p-value of 0.04 so there is around a 4% chance that the next sample we take will be further away from the true conversion rate than the current dataset.”
In my opinion, for the scenario described above, the case for using Confidence Intervals over Significance Scores is overwhelming.
Calculating single proportion confidence intervals
So how do we determine these Confidence Intervals? What analysis allows us to boldly assert an interval of possible values based on a specified confidence level? What calculation method can we use?
Free web-based calculators, simple spreadsheets downloaded from the internet and your old high-school maths teacher are all most likely to just use a normal approximation interval (sometimes referred to as the simple asymptotic method) which has upper and lower bounds given by:
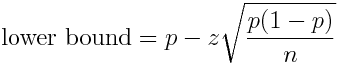
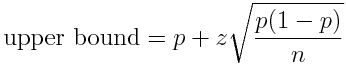
Where n is the sample size, p is the sample proportion and z is the z-value associated with the prescribed confidence level (in Excel we can simply key “NORMSINV(0.95)” to obtain the appropriate z-value for a 95% confidence level).
So, using this method, in the example given in the problem statement we believe that the true conversion lies anywhere in the interval between 0.5% and 3.5% (already quite a difference from 2%!).
In fact, this method is just one example (perhaps the most straightforward) of a bewildering array of means to calculate confidence intervals for a single proportion. In [2] Newcombe gives a far better account of the most widely used of these methods than is feasible for any blog. Crucially he also presents evidence to suggest there are meaningful differences between the results of these methods and, after evidencing its shortcomings, he expresses grave concerns about the accuracy of the above method. In fact Newcombe states:
“it is strongly recommended that intervals calculated by these methods, should no longer be acceptable for scientific literature; highly tractable alternatives are available which perform much better”
To highlight the most easily understood, if not the most significant, problem with the above method consider the case where we have had just 50 clicks and a single conversion. Then, our interval becomes anywhere between -1.3% and 5.3%. Would anyone like to explain to a client why we believe that they could have a negative conversion rate?
Of course, I am highlighting an extreme case and there are means to truncate the intervals but this is just one of the many flaws in the method. Another easily understood problem is that the accuracy suffers badly for more extreme proportions without a very large sample size. Some sources suggest that it ought not to be used whenever np<5 or n(p-1)<5 which would make it unsuitable for our example above.
In any event, if such methods are no longer suitable for scientific analysis, do our clients, who pay for our expertise, deserve to be using them? Given that today’s desktop software allows us to calculate confidence intervals quickly and easily using almost any method we wish, I would suggest not. Our clients deserve the highest feasible level of accuracy and reliability.
The Clopper-Pearson method
As I mentioned above, there are an array of different methods for calculating confidence intervals for a single proportion. I describe just one, the Clopper-Pearson method which Newcombe describes as “the ‘gold standard’ of the strictly conservative criterion”.
It is a conservative method (producing slightly wider confidence intervals than could be expected for other methods) and is accurate for much smaller datasets than other methods. In my opinion this makes this method ideal for the type of significance testing we are likely to need to perform on conversion rates and click-through rates.
Its derivation is firmly beyond the scope of this blog (interested parties can easily find this on Google) however it is a very simple matter to look up the closed-form formulas for the upper and lower bounds then copy the formulas into an excel workbook:
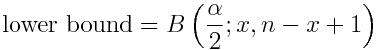
Where B() is the inverse of the Beta Distribution, n is the sample size and x is the number of successes. So, in Excel, for the above example we could simply key:
“BETAINV (1-0.95)/2,5,250-5+1) & BETAINV(1-(1-0.95)/2,5+1,250-5)”
to obtain the lower and upper bounds respectively.
By using such methods we can report to our client that we have seen a conversion rate of 2% so far, but there is not yet enough data to assess the conversion rate accurately. Crucially, we can also confidently (!) report that based on statistical analysis we can be 95% certain that the true conversion rate lies somewhere in the interval between 0.7% and 4.6%.
It is then our client’s decision whether to base decisions on the limited data so far or to wait for a larger sample size – as it always should be. Our part is making sure they have access to and understand the correct analysis on which to base their decision.
Sources: 1. Gardner, M. J., & Altman, D. G. (1986). Confidence intervals rather than P values: estimation rather than hypothesis testing. British medical journal (Clinical research ed.), 292 (6522), 746. 2. Newcombe, R. G. (1998). Two-sided confidence intervals for the single proportion: comparison of seven methods. Statistics in medicine, 17(8), 857-872.