Human beings like to keep things simple. It’s in our nature to do so. This simplification is healthy and natural. It allows us to make sense of the world around us and to describe it to others.
Simplifying complex objects or systems is the essence of mathematical modelling. We need to strip out or simplify the less important parts of a system but retain the most important elements to enable us to gain a better understanding of the overall behaviour.
To highlight the point, consider this beautiful example of modelling from the 1930s. Perhaps it looks familiar?
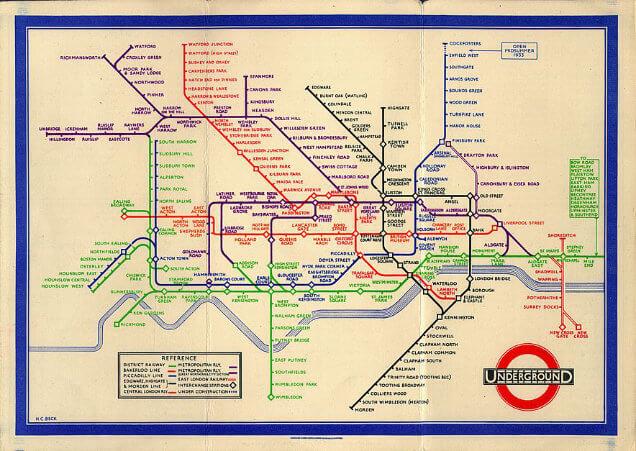
The London Underground map, as we know it today, is still largely based on an innovative model devised by Harry Beck in the 1930s.
Beck’s celebrated insight was that within a transport system (perhaps particularly one which travels underground!) people have little interest in the precise geographical location of the routes they travel and much more interest in how to move efficiently from one station to another. He therefore stripped out the unnecessary detail of the location of the tube lines, and even the precise location of stations, in order to show an incredibly easy to read map of how the stations and routes were interlinked.
The modelling cycle
Most models do not immediately produce such a stark result as Beck’s Tube map. Remembering his example provides inspiration for our end goal but it gives little or no clue as to how to get there. So how does one go about building a model?
Whenever I try to build a mathematical model, I make a point of remembering a diagram from one of my university textbooks that looked similar to this:
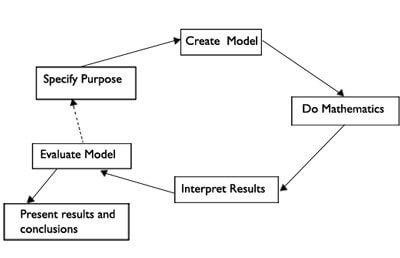
This, for me, is an important visualisation of the process that I always recall.
I make a point of remembering it because it reminds me to not miss out any of the stages. It sounds ludicrous, but it is very easy to forget to specify the purpose of the model we are building and jump straight into trying to fit lines to data and describing mathematical relationships.
The first stage cannot and must not be skipped. There is no sense trying to rely on a purpose we believe is ‘inherent’ or ‘implied’ by the nature of the system we are modelling. We must be absolutely clear as to what the purpose of our model is. Without a clearly defined purpose, we cannot hope to make the right decisions on the details that we need to include in our model.
The purpose we choose should be specific, clear and simple. For example, when devising a model for PPC bid management I could specify that:
The model should describe the relationship between bid price and profit in order to enable the optimum bid price that maximises returns to be found.
There are many other parameters I could look at in an endeavour to maximise returns (ad texts, landing pages, etc.) and many other metrics influenced by bid prices (consider its effect on position, CPA, ROI, etc.).
These may or may not relate to my purpose. Such concerns are not important at this stage. All extraneous parameters are deliberately omitted from the stated purpose. We may end up measuring these things in our model; we may have to, but the point is that now we have a clear purpose we can take an informed decision on whether they add value to delivering on the purpose of our model.
We should be cautious here to keep the scope of our model as narrow as possible. By specifying the purpose so clearly and narrowly I can have a much better chance of making the best assumptions to focus on the end goal rather than getting bogged down modelling irrelevant or insignificant parts of the system.
On a similar note, it is very easy to forget the final stage of our cycle. We can specify the purpose of our model, make some sensible assumptions and do lots of splendid data analysis and mathematical work but unless we interpret the results and measure their fit with the real world, unless we test those ‘sensible’ assumptions with real data, we can never hope for our model to be of any practical use.
Making assumptions in order to simplify the model
When we say ‘build the model’, what we really mean is the simplification process I discussed in the introduction. We need to make sensible assumptions about the system we are modelling in order to reduce the number of variables or to simplify their relationship with one another.
This can be a very difficult and counter-intuitive task. For example, one of the things Beck assumed was that the underground lines are all laid in straight lines along North-South, East-West or at a 45º angle to these! In the real world this would plainly be an absurd assumption – but for the purpose of his model, making this assumption allows Beck to give us a much clearer impression of how the stations are interlinked than he would have been able to by following the actual rail routes.
In order to highlight the difference, consider this tube map using all the familiar colours, symbols and names but with a little more geographical accuracy:
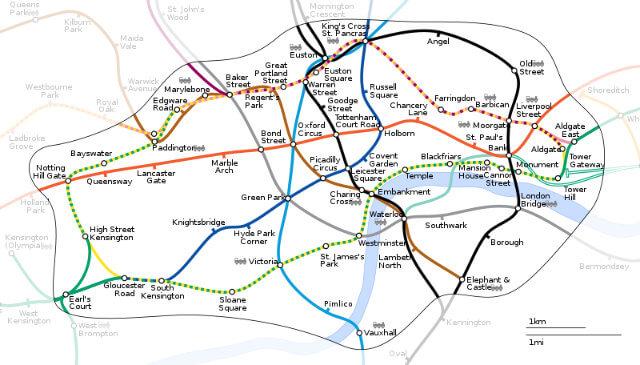
Nobody could doubt that the above map contains more data than Beck’s map (or its modern equivalent) but which one would you rather have in your pocket if you were a stranger to London and needed to get from Finsbury Park to Blackfriars?
We can, and do, make comparable assumptions in PPC when we try to model the relationship between bid price and profit. We could, for example, quite sensibly assume that the conversion rate is constant for each keyword and ad text irrespective of what position it appears.
Doing so doesn’t imply that we think position could NEVER influence conversion rate any more than Beck believed that the train tracks were actually laid out as shown on his map! We must make simplification assumptions in order to build a working model and there are usually much more important parameters to consider.
One useful technique here is to list all the parameters that could possibly have any affect on the model and then attempt to prioritise them as to how likely each would be to affect the output, then relate these back to the specified purpose and make assumptions to eliminate or assimilate all but the top couple of parameters.
Of course, when we get to the stage of evaluating the results we may need to re-consider our assumptions but, by then, we will know more about the key relationships and perhaps have a better idea of how to amend those assumptions. In an initial build, we cannot be afraid to make bold assumptions in order to simplify relationships – just as Beck did.
Above all, let us remember that mathematical modelling is a cyclic process. We hope to improve the quality of our model on every iteration of the process by testing and re-examining the assumptions we made in order to produce the previous one. If we find that one of our assumptions was inaccurate or simplified matters too far, we can amend it at the next iteration when we have examined the result and have some solid analysis on which to base the next assumption.


