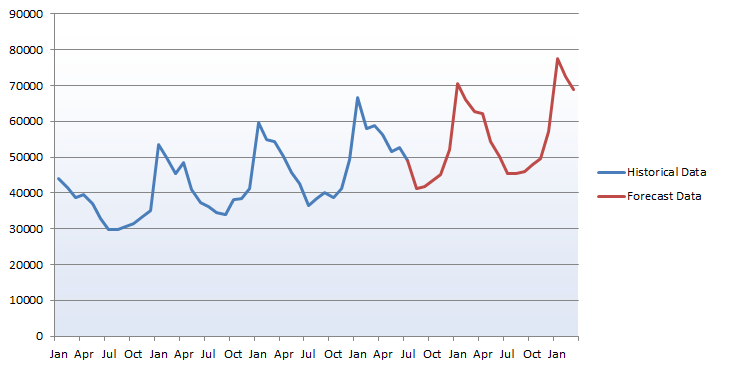
The title may sound complicated, but all it refers to is a means of explaining a signal (i.e. page hits, conversions, etc.) over time and taking into account a seasonal or cyclical element. This can be useful in explaining why a metric appears to be declining in the short-term, only to pick up in the long-term, and may help to shed light on why this has happened. To decompose a time series is to break it down into constituent elements – here we are looking at three components:
- An underlying trend e.g. the long-term growth rate of the signal
- A seasonal element – the fluctuations over time, which may be annual, quarterly, monthly, or in the space of a single day
- A noise element – random behaviour which we cannot attribute to the above
For the example data I will use (which is purely for illustrative purposes), we are looking at web traffic which has a strong seasonal component. The seasonal element was apparent over an annual period, with high volumes of hits in January, and more level volumes through the rest of the year with a lull in the summer months. Year on year growth is also evident.
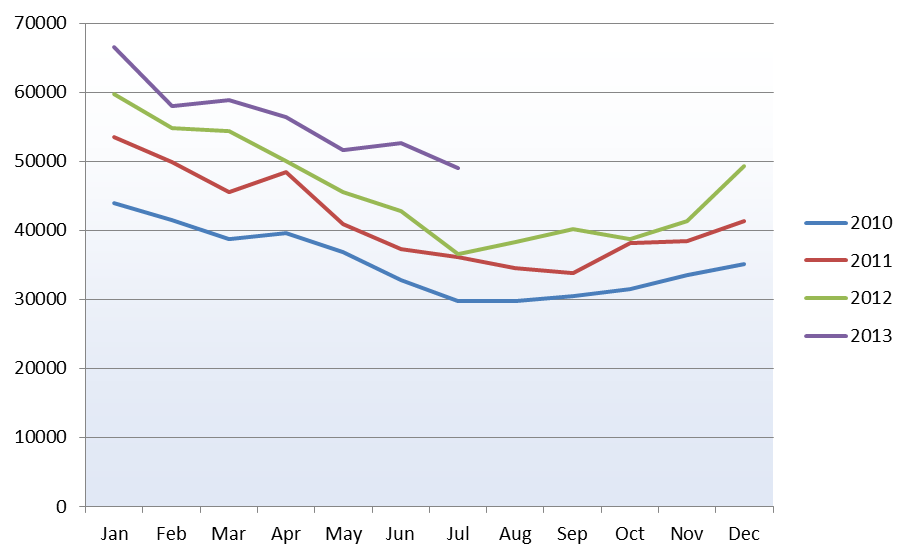
In order to break down the data, we need to find the underlying growth trend, and the seasonal trend.
Step one
Firstly we smooth out the data over the year using a weighted moving average (MA). As the trend is annual, the moving average must include data points from all months of the year. This will give us the underlying growth component, and from there we can calculate the seasonal component.
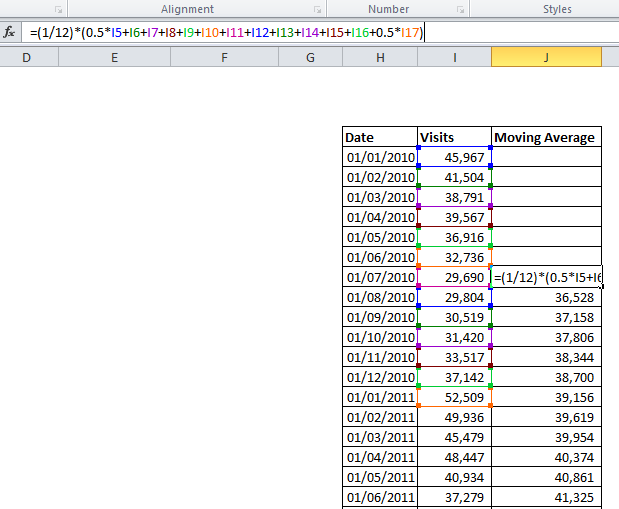
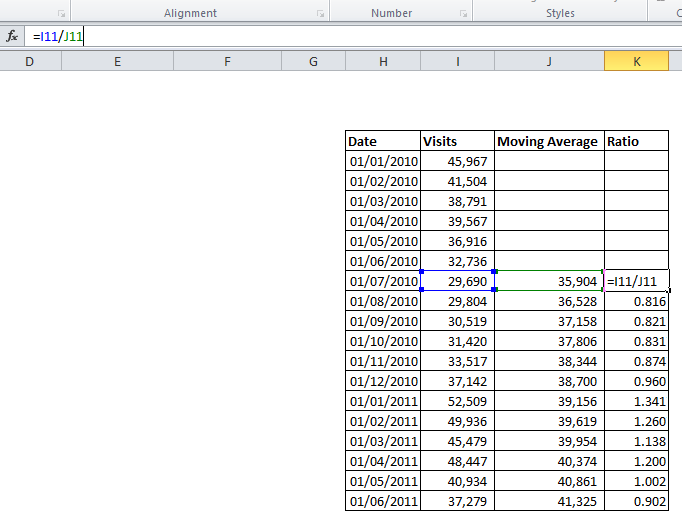
In the example, I produce an average sales value for each month by averaging over the six months either side of it, to produce a centred moving average of order 12. For July, January is included twice, so we halve those values, then divide by 12 to obtain a monthly figure. Necessarily we lose some data from the start of the sample, where there are not six preceding months.
Step two
The next step requires us to choose whether a multiplicative or additive model is suitable. In a multiplicative decomposition, the seasonal element varies according to the underlying growth, whereas in an additive model it remains consistent in size. This can normally be gauged from the graph.
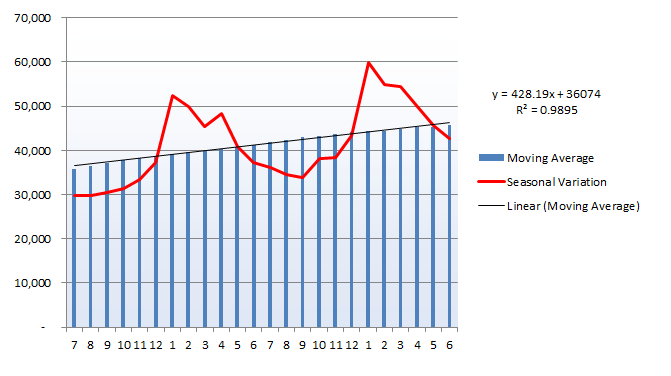
In the chart above, it can be observed that the seasonal differences in later years, when traffic is higher are greater – this suggests a multiplicative model is required.
We can now calculate the ratio between the moving average, and the raw figures. This is simply the raw figure divided by the corresponding MA figure (in an additive model, we would find the difference rather than the ratio). As shown below, this gives a series of numbers either side of one – in August, just 0.816 of the long term traffic was observed, while in January 1.341 times the long-term average was recorded – as we would expect having seen on the initial graph how the seasonal fluctuation affects this data.
Step three
Above we only see values for July 2010 through to June 2011 – in the actual analysis we would use the whole available dataset, giving multiple values for each month. We should then average these out (e.g. average the January figures together, then the February etc.) to obtain more reliable seasonal coefficients and smooth out some of the noise in the data.
As we are working with ratios, the difference in the absolute values between say October 2008 and October 2012 does not affect the calculation. This can be done using Excels “AVERAGEIF” function:
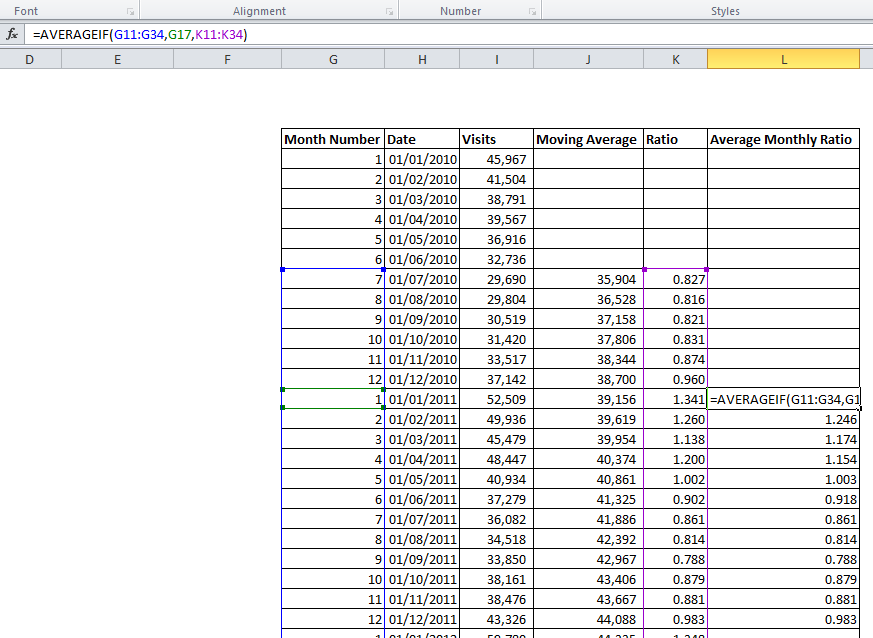
We now have a separate ratio for each month of the year. These should now be scaled to ensure their average is one (depending on the dataset used, it may not be). To do this, divide each monthly figure by the average of all 12. This ensures we are not inflating or deflating the raw figures when adjusting for seasonality – the 12 values must sum to 12, thus averaging one.
Step four
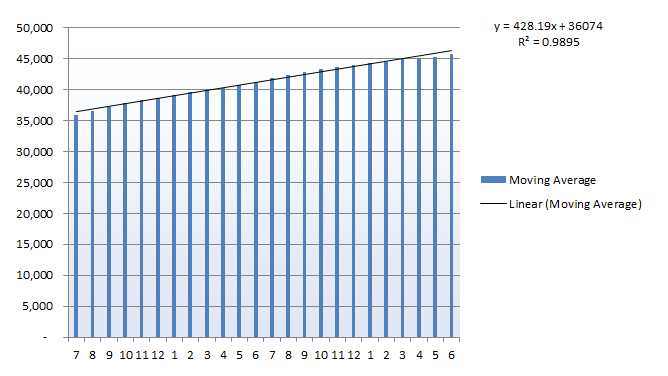
Lets now have a look at the underlying growth trend – we need to find the average monthly increase in traffic. Using the Moving Average data we have created, plot a chart and add a trend-line.
Here, the linear trend-line provides a very close fit, with an R2 value close to one. The equation on the chart tells us that, starting at a base of 36,074, this data has subsequently seen an average growth of 428 visits per month over the assessed period. Other datasets may show a quadratic, exponential or more complex growth trend.
The analysis we have done would enable us to measure long term growth, and also explain the seasonal variation in quantitative terms. In some industries, seasonal fluctuations may be easily explained – consider ice cream manufacturers, or producers of Christmas decorations. Sometimes the seasonal element may be more subtle though – and remember, seasonal trends arent restricted to Spring/ Summer/ Autumn/ Winter – differences in site traffic over the course of an individual day may also benefit from this analysis.
The seasonal variation line above plots the raw data for each month, showing how we have smoothed out the peaks and troughs over the twelve month cycle to arrive at a long term average.
We can also use this average growth figure to predict future growth, and adjust on a monthly basis using the seasonal parameters we have determined.
Step five
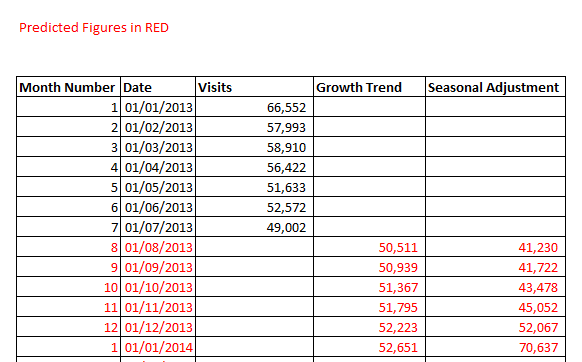
We can now produce a simple and approximate forecast for future months performance quite easily. For each subsequent month, add on the 428 visits we have determined is the underlying growth rate, and multiply by the appropriate monthly coefficient.
For the first month to be predicted, I have used the average of the 12 previous months as a baseline value. The Growth Trend column then adds on 428 visits each month, and the Seasonal Adjustment multiplies this figure by the monthly coefficient we have calculated.
Here we see the forecast figures against the historical data we have used. It appears we have preserved the overall trend, while paying particular attention to the seasonal spikes and troughs through the year.
This method can give us an approximation of the signal for future months. It should be remembered though that each forecast month is based on the previous prediction, and so this trend could go awry if hitherto unconsidered factors become involved. More advanced analysis could produce a 95% confidence interval for each forecast, and would typically use exponential smoothing or another method more powerful than time series decomposition.
To sum up…
Sometimes time series data can display what appear to be obvious trends, as in the final graph above. While a pattern of growth and a fairly regular seasonal pattern are visible, it may be hard to explain this data as an overall trend. Breaking down the series into different components may allow easy modelling of each part; in this example we have arrived at the overall growth rate and seasonal coefficients for each months impact on this. Going further, we may attempt to uncover any cyclical trends such as the longer- term economic cycle, or use more sophisticated methods to allow more accurate forecasting to be carried out.
Are you interested in taking your time series decomposition data further? Learn how our Analytics and Data Science teams can help you do it.