To advance on my previous VBA blog on writing custom functions, I am going to show how to write the other fundamental building block of VBA code, a “Sub” – short for subroutine.
While a function produces an output value based on inputs and processes defined within it, a sub may affect any aspect of Excel, writing outputs to the sheet and calling other functions or subs as it executes. We are going to write a short sub to solve the following problem:
How can Pi be calculated by dropping pins?
Calculation of Pi in this way is an old method to find an approximate value, and relates to a similar problem known as Buffons Needle. The concept is based on finding the ratio between the number of dropped pins landing inside or outside a circle of radius 1 drawn within a square of edge length 2.
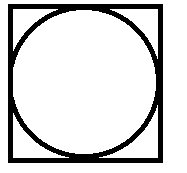
Imagine randomly dropping 100 pins into the square – we would expect most to land inside the circle, and the rest outside it – perhaps 78 inside, and 22 outside. Thus, we could conclude that the circle has an area approximately the size of the square. The square has area 2 * 2 = 4 units, so our approximate area for the circle is (78/100) * 4 = 3.12. As the circle has radius 1, its area is given by the formula: A = Pi , so A=Pi , and our approximation for Pi is 3.12. Most people will remember that Pi is 3.14 to 2 decimal places, so we are fairly close.
To get closer to the true value of Pi, we must drop more pins. 1000 pins dropped may result in 785 landing within the circle, and 215 outside. Following the same logic as above, gives 3.14 – so we are now accurate to 2 decimal places. However, for most practical uses greater accuracy is required – this is where computer simulation takes over, as no one wants to drop, and then count, thousands of pins!
Writing a VBA sub
We are going to replicate the above practical experiment in VBA code. This will allow us to set the number of dropped pins to any value our computer can handle, and compute Pi to the required accuracy. This will introduce a number of VBA/ programming concepts.
Our sub will be an example of a Monte Carlo simulation – repeating a test many times to refine the answer produced by it. We are simulating dropping pins by using Excels random number generator to create landing co-ordinates for each pin, then counting the virtual pins landing inside the unit circle.
To begin, we will name our sub and define some variables to be used later. The below code should be entered into an Excel VBA code module. To do this, open Excel, press ALT+F11 to open the VBA editor, right-click on the filename in the Project Explorer window and choose Insert>Module.

This code names our sub as ‘calcPi’, and the empty brackets after the name indicate it doesn’t require any input parameters. The ‘Dim’ statements tell the computer how much memory to reserve for each variable, depending on its type. We have two types, ‘Long’ which is used for large integer values, and ‘Double’ which can take decimal values. We have also set N to the value 100,000 – this will be the number of pins dropped in the simulation.

The next piece of code sets up our pin drops. The VBA command ‘Randomize’ seeds the random number generator in Excel, allowing different random numbers to be generated each time the code is run. We then set up a ‘For Loop’ – this is an instruction telling the code to run in a loop. We have a control variable called ‘iteration’, which will count the loops as they occur, and have set the loop to run from 1 to N, to which we have assigned the value 100,000. So, the code will repeat 100,000 times. The variables x and y are assigned random numbers between 0 and 1.

We now test whether the random numbers assigned – simulating the dropping of a pin onto the square – fall inside the unit circle or not. We use Pythagoras Theorem to determine where the pin landed – if , then the pin is further than 1 unit from the centre – and therefore outside of the circle. Above, we use an If statement to test for this, and if the distance is less than 1, we increase the piCount variable by 1.
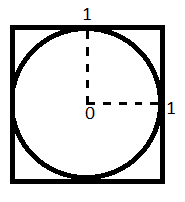
To do this, we are making a simplification on our original diagram. Our x and y co-ordinates may only take values from 0 to 1 – this is the default for the random number generator. This means they may only fall in the top right quadrant of the diagram. However, the proportional sizes of inside/ outside the circles are the same as when the full circle/ square is considered.
The final lines of code are above. Once the For Loop has been repeated N times, as we set up before, the approximation to Pi is calculated as we did in the manual version. ‘piCount/ N’ works out the proportion of pins landing inside the circle, and we multiply by 4 to get the value over the whole area of the diagram. ‘MsgBox’ tells Excel to produce a dialogue box, and we display the value of ‘piVal’ within it. ‘End Sub’ lets Excel know that we have reached the end of the code.
The full code


To run this, place your cursor somewhere within the code and press F5. Excel will then display a message box showing the calculated value of Pi – this may take a couple of seconds or more, depending on your computer. You will hopefully get a value close to 3.1415 – the true value of Pi to 4 decimal places. However, you may still be a little way off – this is where computation of simulated experiments like this shows its real strength. We may increase the value of N by 10 or 100 times by adding zeroes to the end, and then run the code. It will take longer to run but should get us a more accurate answer as the number of virtual pins is increased. If you encounter an error in your code, or would like to know what is happening at each stage of the execution, I will cover this in the next blog.
In this blog we have seen the Random command, a For Loop, an If Statement, and a MsgBox command. These are all we need to convert a real-life problem into a computer model, which we can simulate many times to improve accuracy. We can do this step by step:
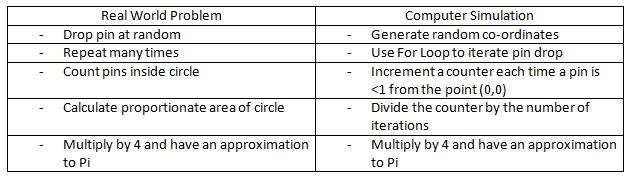
Hopefully this method shows how practical problems may be modelled as simulations. Whilst this example isn’t directly applicable to Search Engine Marketing (and Excel has a Pi constant built in), familiarity with the different VBA commands can make a lot of real world problems easy to convert into computational problems.



